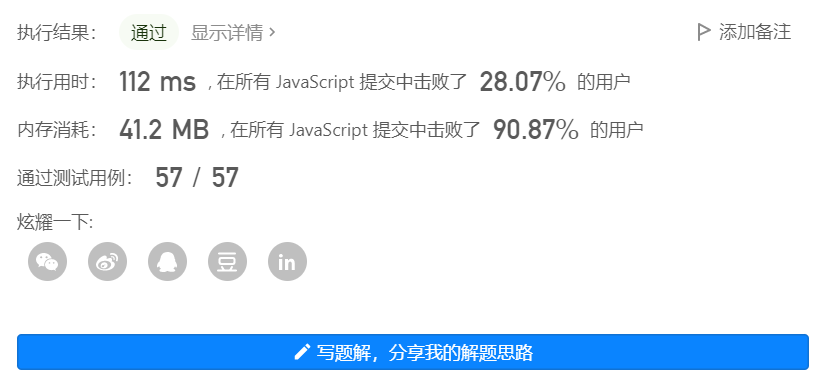
1. 两数之和
https://leetcode.cn/problems/two-sum/
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var twoSum = function(nums, target) {
let result = []
for (let i = 0; i<nums.length; i++) {
for (let j = i+1; j<nums.length; j++) {
if (nums[i]+nums[j]===target) {
result = [i,j]
break
}
}
}
return result
};
15. 三数之和
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
let result = []
let arr = nums.sort((a, b) => {return a - b})
for (let i = 0; i<arr.length; i++) {
if (i>0 && arr[i] === arr[i-1]) continue
for (let j = i+1; j<arr.length; j++) {
if (j>i+1 && arr[j] === arr[j-1]) continue
for (let k = j+1; k<arr.length; k++) {
if (arr[i]+arr[j]+arr[k] === 0) {
if (k>j+1 && arr[k] === arr[k-1]) {
k++
continue
}
result.push([arr[i], arr[j], arr[k]])
}
}
}
}
return result
};
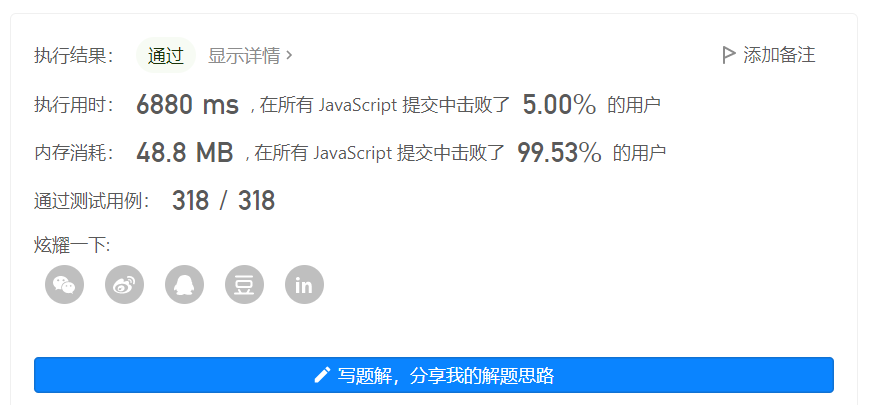
5%……我裂开……思路还是for暴力循环,但是和上面的耗时过长做了一个先把数组排序的操作。
感觉肯定是有简单的方法的…
但肯定都是定一移二的操作
18. 四数之和
/**
* @param {number[]} nums
* @param {number} target
* @return {number[][]}
*/
var fourSum = function(nums, target) {
let result = []
let arr = nums.sort((a, b) => {return a - b})
for (let i = 0; i<arr.length; i++) {
if (i>0 && arr[i] == arr[i-1]) continue
for (let j = i+1; j<arr.length; j++) {
if (j>i+1 && arr[j] == arr[j-1]) continue
for (let k = j+1; k<arr.length; k++) {
if (k>j+1 && arr[k] == arr[k-1]) continue
for (let l = k+1; l<arr.length; l++) {
if (arr[i]+arr[j]+arr[k]+arr[l]===target) {
if (l>k+1 && arr[l] === arr[l-1]) {
l++
continue
}
result.push([arr[i],arr[j],arr[k],arr[l]])
}
}
}
}
}
return result
};
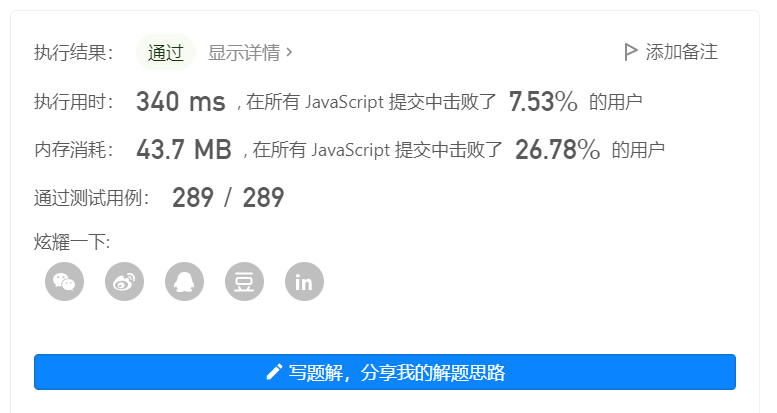

评论区