Huffman编码算法

问题描述

压缩算法，目的就是根据字母的出现频率来“按需分配”编码来优化编码方式。

比如：给出一串字母 Huffman Coding   ，按照计算机处理形式，会根据ascll码将这串字符编码，具体形式（十进制）就是104 117 102 102 109 97 110 32 67 111 100 105 110 103，然后转换成二进制，最后会得到需要97个比特来存储。

算法描述

算法角度来讲对上述问题ascll编码方式是浪费空间的，优化方向是改变编码方式，根据字母出现的频率来“按需分配”进制位。

给出下面所给出的字母，以及出现的频率，来得到哈夫曼编码

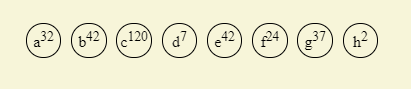
先提出将频率小的依次加入。d和h组合权值为9(或者说A只是称呼方便)，然后将这个9“替换d和h”代入整个序列，在进行插入树操作，

在进行到E的时候，此时的队列应该为120 107 42 37，所以此时需要重新调整队列，然后进行到结束。

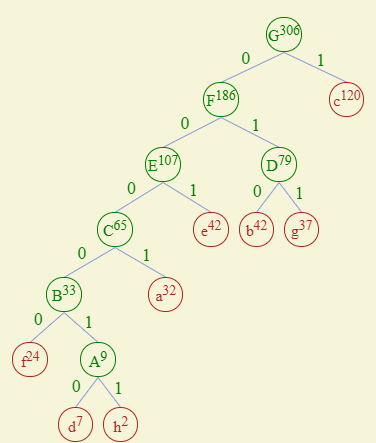
最后的编码结果为：

编码实现

#include <stdio.h>
#include <vector>
#include <algorithm>
namespace NS_HuffmanCoding {
using namespace std;
void BuildHuffmanTree();
void Initialization(vector<pair<char, int>> chars);
void Finalization();
struct HFMNode {
  char Ch; int Freq;
  HFMNode* Left, * Right;
  HFMNode(char pCh, int pFreq, HFMNode* pLeft, HFMNode* pRight)
    : Ch(pCh), Freq(pFreq), Left(pLeft), Right(pRight) {}
  HFMNode(char pCh, int pFreq)
    : HFMNode(pCh, pFreq, NULL, NULL) {}
};
void MinHeapify(vector<HFMNode*>& H);
void InsertH(vector<HFMNode*>& H, HFMNode* node);
void SiftDown(vector<HFMNode*>& H, int i);
void SiftUp(vector<HFMNode*>& H, int i);
HFMNode* ExtractMin(vector<HFMNode*>& H);
void DeleteANode(HFMNode* node);
void ShowInput(vector<pair<char, int>> chars);
void Output();
static vector<HFMNode*> Q;
void HuffmanCodingCaller(vector<pair<char, int>> chars)
{
  ShowInput(chars);
  Initialization(chars);
  BuildHuffmanTree();
  Output();
  Finalization();
}
void BuildHuffmanTree()
{
  char C = 'A';
  while (Q.size() > 1)
  {
    HFMNode* x = ExtractMin(Q);
    HFMNode* y = ExtractMin(Q);
    HFMNode* z = new HFMNode(C++, x->Freq + y->Freq, x, y);
    InsertH(Q, z);
  }
}
HFMNode* ExtractMin(vector<HFMNode*>& H)
{
  swap(H.front(), H.back());
  HFMNode* p = H.back();
  H.pop_back();
  if (!H.empty())
    SiftDown(H, 0);
  return p;
}
void SiftDown(vector<HFMNode*>& H, int i)
{
    while ((i = (i << 1) + 1) < H.size()) {
        if ((i + 1 < H.size()) && (H[i + 1]->Freq < H[i]->Freq))
            i = i + 1;
        if (H[(i - 1) >> 1]->Freq > H[i]->Freq)
            swap(H[(i - 1) >> 1], H[i]);
        else break;
    }
}
void InsertH(vector<HFMNode*>& H, HFMNode* node)
{
  H.push_back(node);
  SiftUp(H, H.size() - 1);
}
void SiftUp(vector<HFMNode*>& H, int i)
{
  while (i > 0 && H[i]->Freq < H[(i - 1) >> 1]->Freq) {
    swap(H[i], H[(i - 1) >> 1]);
    i = (i - 1) >> 1;
  }
}
void MinHeapify(vector<HFMNode*>& H)
{
  for (int i = (H.size() >> 1) - 1; i >= 0; i--) {
    SiftDown(H, i);
  }
}

void Initialization(vector<pair<char, int>> chars)
{
  Q.clear();
  for (auto ch : chars)
    Q.push_back(new HFMNode(ch.first, ch.second));
  MinHeapify(Q);
}
void Finalization()
{
  DeleteANode(Q[0]);
}
void DeleteANode(HFMNode* node)
{
  if (node->Left)
  {
    DeleteANode(node->Left);
    DeleteANode(node->Right);
  }
  delete node;
}
void ShowInput(vector<pair<char, int>> chars)
{
  printf("Huffman coding input: \n");
  for (auto c : chars)
    printf("%c,%d; ", c.first, c.second);
  printf("\n");
}
static vector<char> coding;
static vector<pair<char, vector<char>>> codingList;
void GetHuffmanCoding(HFMNode* node)
{
  if (node->Left)
  {
    coding.push_back(‘0’);
    GetHuffmanCoding(node->Left);
    coding.pop_back();
    coding.push_back(‘1’);
    GetHuffmanCoding(node->Right);
    coding.pop_back();
  }
  else
  {
    codingList.push_back(pair<char,
      vector<char>>(node->Ch, coding));
  }
}
void Output()
{
  printf("Huffman coding:\n");
  coding.clear();
  codingList.clear();
  GetHuffmanCoding(Q[0]);
  sort(codingList.begin(), codingList.end());
  for (auto c1 : codingList)
  {
    printf("  %c: ", c1.first);
    for (auto c2 : c1.second)
      printf("%c", c2);
    printf("\n");
  }
  printf("\n");
}
} //namespace NS_HuffmanCoding
using namespace NS_HuffmanCoding;
void TestHuffmanCoding()
{
  vector<vector<pair<char, int>>> charLists = {
      //Introduction to Algorithms
     {
        { {‘a’,40}, {‘b’,13}, {‘c’,12},
          {‘d’,16}, {‘e’,9}, {‘f’,5} },
     },
     //ÑÏεÃô
     {
        { {‘a’,5}, {‘b’,29}, {‘c’,7}, {‘d’,8},
          {‘e’,14}, {‘f’,23}, {‘g’,3}, {‘h’,11} },
     },
  };
  int n = charLists.size();
  for (int i = 0; i < n; i++)
  {
    HuffmanCodingCaller(charLists[i]);
  }
}