0-1背包问题

问题描述

问题描述

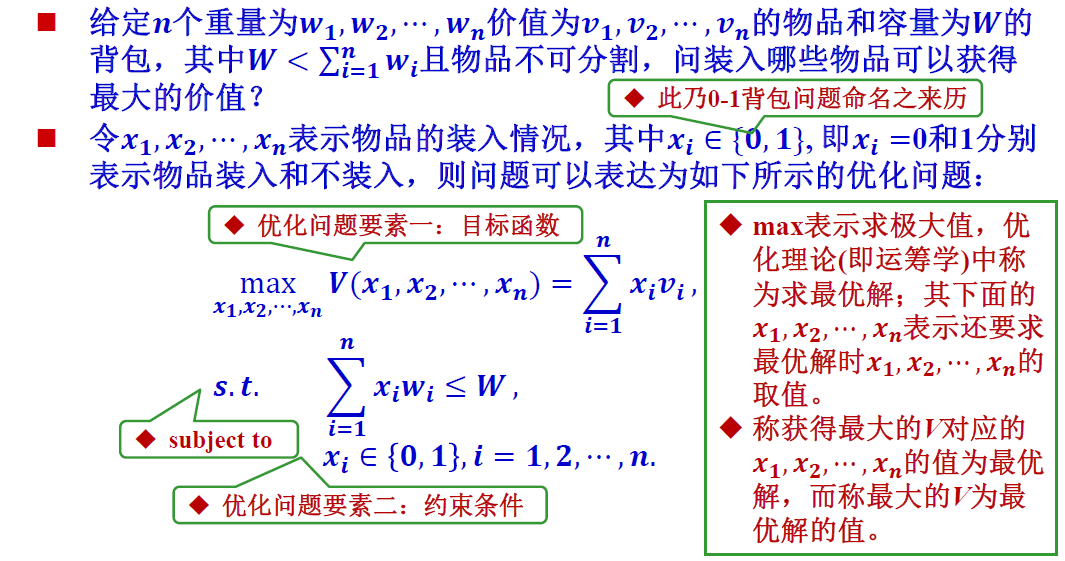
给定一组已知重量和价值的物品和一个容量已知的背包，求解在不超过背包容量情况下，选用那些物品放入背包，使得所选用的所有物品价值最大化。

问题的判定性说法

问题的形式化定义

问题思路

动态规划思路

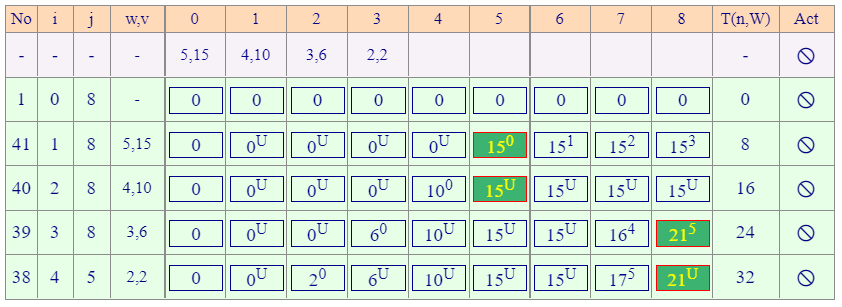
动态规划解决该问题，类似于莱文斯坦距离的解法类似。利用CAAIS数据来说明这个问题的解决思想。

动态规划DP方程构造

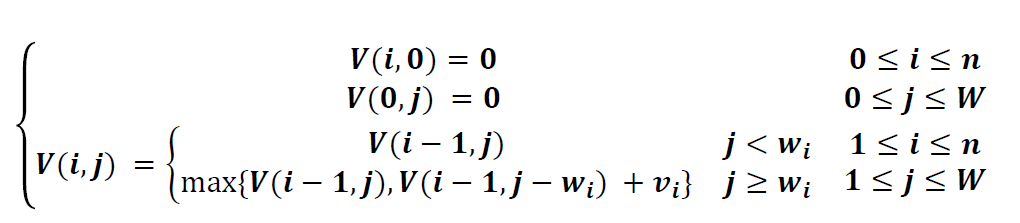
PS：V[i,j]表示在前i件物品中选择若干件放在承重为 j 的背包中，可以取得的最大价值

（整张表格是从上往下，从左往右地填）

举例说明表格中的数值填法，倒数第二行倒数第四列的16 4的填法：

• 首先不满足DP方程的第一种和第二种情况
• 所以代入取最大值max函数

• V（i-1，j）：不选本物品（3，6），还是用之前的值，继承上面的第一个物品和第二个物品，DP值为15 U
• V（i-1，j）+vi：用该容量（7）-所选物品的重量为4，然后再查容量为4的时候DP值为10，然后求出该情况DP是，10加上该物品的价值，所以该情况下的DP值为16，右上标为4（CAAIS），值来源于前面容量为4的情况。

格子如上方式填就好了！

递归思路

第二节课将递归的时候，也讲了这个问题的递归思路。不过复杂度记得是指数级的，暂时不写了~~

代码实现

动态规划Code

#include <iostream>
#include <vector>
using namespace std;
namespace NS_DP0_1Knapsack {
int DP0_1Knapsack(int n, int W, int *w, int *v);
void Output(int n, int W, int *w, int *v, int OptV);
static vector<vector<int>> V;
static vector<int> x;
void DP0_1KnapsackCaller(int n, int W, int *w, int *v)
{
    V.clear();
    V.resize(n + 1, vector<int>(W + 1, 0));
    x.resize(n + 1);
    int OptV = DP0_1Knapsack(n, W, w, v);
    Output(n, W, w, v, OptV);
}
int DP0_1Knapsack(int n, int W, int *w, int *v)
{
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= W; j++)
            if (j < w[i - 1])
                V[i][j] = V[i - 1][j];
            else if (V[i - 1][j] >=
                V[i - 1][j - w[i - 1]] + v[i - 1])
                V[i][j] = V[i - 1][j];
            else
                V[i][j] = V[i - 1][j - w[i - 1]] + v[i - 1];
    int j = W;
    for (int i = n; i > 0; i--)
        if (V[i][j] == V[i - 1][j])
            x[i] = 0;
        else
        {   x[i] = 1; j -= w[i - 1];  }
    return V[n][W];
}
void Output(int n, int W, int *w, int *v, int OptV)
{
    //inputs
    printf("DP to solve 0-1 knapsack:\n");
    printf("%d items with knapsack capacity %d.\n", n , W);
    printf("%-6s: ", "Weight");
    for (int i = 0; i < n; i++)
        printf("%3d", w[i]);
    printf("\n");
    printf("%-6s: ", "Value");
    for (int i = 0; i < n; i++)
        printf("%3d", v[i]);
    printf("\n");
    //the value matrix
    printf("\nThe value matrix:\n");
    printf("  ");
    for (int j = 0; j <= W; j++)
        printf("%3d", j);
    printf("\n");
    for (int i = 0; i <= n; i++)
    {
        printf("%2d", i);
        for (int j = 0; j <= W; j++)
            printf("%3d", V[i][j]);
        printf("\n");
    }
    //solution
    printf("\nThe optimal value: %d\n", OptV);
    printf("The optimal solution:\n");
    for (int i = 1; i <= n; i++)
        printf("%2d", x[i]);
    printf("\n\n");
}
} //namespace NS_DP0_1Knapsack
using namespace NS_DP0_1Knapsack;
int main()
{
    // 物品个数
    vector<int> N = { 4,  10};
    // 背包容量
    vector<int> W = { 8,  100};
    // 各物品重量
    vector<vector<int>> w = {
        { 5, 4, 3, 2 },
        { 4, 3, 7, 2, 9, 3, 1, 7, 2, 5 }
    };
    // 各物品价值
    vector<vector<int>> v = {
        { 15, 10, 6, 2 },
        { 15, 10, 6, 2, 23, 12, 33, 7, 22, 10 }
    };

    int m = N.size();
    for (int i = 0; i < m; i++)
    {
        DP0_1KnapsackCaller(N[i], W[i], &w[i][0], &v[i][0]);
    }

    return 0;
}

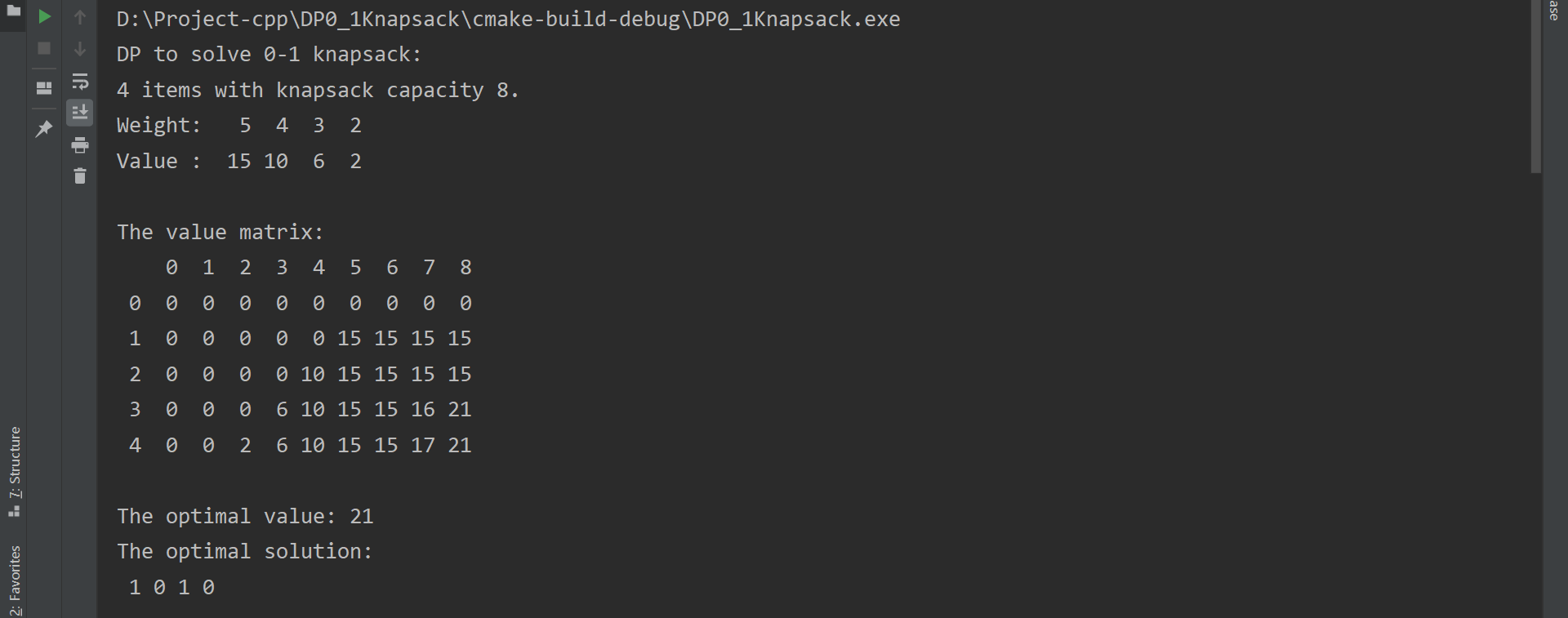
动态规划Result